Jeśli kiedykolwiek zwróciłeś uwagę na układ liści na łodydze rośliny, teksturę ananasa lub łupiny szyszki, przypadkowo byłeś świadkiem pięknych przykładów matematycznych wzorów w przyrodzie.
Tym, co łączy wszystkie te cechy roślin, jest ich wspólna cecha ułożenia w spirale przylegające do sekwencji numerycznej zwanej ciąg Fibonacciego.
Dla uproszczenia nazywane spiralami Fibonacciego, spirale te są wszechobecne w roślinach i fascynowały naukowców od Leonarda da Vinci po Karola Darwina.
To jest rozpowszechnienie spiral Fibonacciego w dzisiejszych roślinach i uważa się, że to reprezentuje Bardzo stara i zastrzeżona funkcjasięgające najwcześniejszych stadiów rozwoju roślin i kontynuujące w obecnych formach.
Jednak mamy Nowe badanie kwestionuje ten punkt widzenia. Zbadaliśmy spirale w liściach i strukturę reprodukcyjną skamieniałej rośliny sprzed 407 milionów lat.
Co zaskakujące, odkryliśmy, że nie wszystkie spirale zaobserwowane u tego konkretnego gatunku podlegały tej samej zasadzie. Obecnie bardzo niewiele roślin nie podąża za wzorem Fibonacciego.
Czym są spirale Fibonacciego?
Spirale występują często w przyrodzie i można je zobaczyć w liściach roślin, skorupach zwierząt, a nawet w podwójnej helisie naszego DNA. W większości przypadków spirale te są powiązane z ciągiem Fibonacciego – zbiorem liczb, z których każda jest sumą dwóch poprzedzających ją liczb (1, 1, 2, 3, 5, 8, 13, 21 itd.).
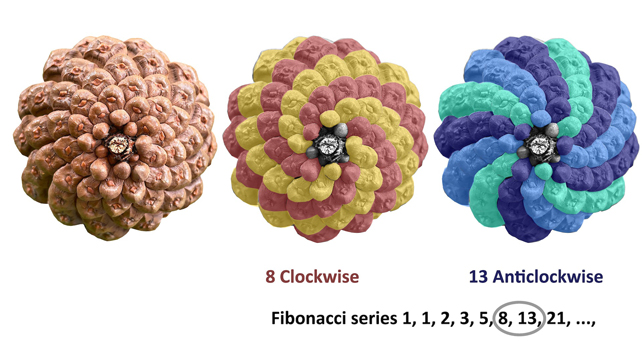
Wzory te są szczególnie rozpowszechnione u roślin i można je rozpoznać gołym okiem. Jeśli podniesiesz szyszkę i spojrzysz na podstawę, zobaczysz zdrewniałe łuski tworzące spirale, które zbiegają się w kierunku punktu przyczepienia do gałęzi.
Na początku możesz dostrzec spirale tylko w jednym kierunku. Ale przyjrzyj się uważnie, a zobaczysz obie spirale zgodnie z ruchem wskazówek zegara i przeciwnie do ruchu wskazówek zegara. Teraz policz liczbę spiral zgodnie z ruchem wskazówek zegara i przeciwnie do ruchu wskazówek zegara, a prawie w każdym przypadku liczba spiral będzie liczbami całkowitymi w ciągu Fibonacciego.
Ten konkretny przypadek nie jest przypadkiem wyjątkowym. W Stań który przeanalizował 6000 szyszek, spirale Fibonacciego znaleziono w 97 procentach zbadanych szyszek.
Spirale Fibonacciego istnieją nie tylko w szyszkach sosnowych. Są powszechne w innych organach roślin, takich jak liście i kwiaty.
Jeśli przyjrzysz się czubkowi liściastego liścia, na przykład małpiego drzewa puzzli, zobaczysz, że liście są ułożone spiralnie, zaczynając od czubka i stopniowo owijając się wokół łodygi. A Stań Spośród 12 000 spiral z ponad 650 gatunków roślin, spirale Fibonacciego występują w ponad 90 procentach przypadków.
Ze względu na częstość ich występowania w żywych gatunkach roślin od dawna uważa się, że spirale Fibonacciego były starożytne i wysoce zachowane we wszystkich roślinach. Postanowiliśmy przetestować tę hipotezę, badając skamieniałości wczesnych roślin.
Spirale inne niż Fibonacciego we wczesnych roślinach
Zbadaliśmy rozmieszczenie i rozmnażanie liści w pierwszej grupie roślin, o których wiadomo, że rozwinęły liście, tzw Klub Alg.
W szczególności zbadaliśmy skamieniałości roślin wymarłych gatunków alg Maki Astroxylon. Skamieniałości, które badaliśmy, znajdują się obecnie w zbiorach muzeów w Wielkiej Brytanii i Niemczech, ale zostały pierwotnie zebrane Rainey Chert Miejsce skamieniałości w północnej Szkocji.

Zrobiliśmy zdjęcia cienkich warstw skamieniałości, a następnie wykorzystaliśmy cyfrowe techniki rekonstrukcji, aby zwizualizować układ A. MakjiLiście w 3D i identyfikuj ślimaki.
Na podstawie tej analizy odkryliśmy, że układ liści był bardzo zmienny A. Makji. W rzeczywistości najpowszechniejszym układem były spirale inne niż Fibonacciego. Odkrycie spiral innych niż Fibonacciego w tak wczesnych skamielinach jest zaskakujące, ponieważ są one tak rzadkie wśród żyjących obecnie gatunków roślin.
Charakterystyczna historia ewolucji
Odkrycia te zmieniają nasze rozumienie spiral Fibonacciego w roślinach lądowych. Sugerują, że spirale inne niż Fibonacciego były starożytne w mchach, obalając pogląd, że wszystkie rośliny liściaste zaczęły wyrastać z liści zgodnych ze wzorem Fibonacciego.
Co więcej, wskazuje to, że ewolucja liści i spiral Fibonacciego u mchów klubowych miała historię ewolucyjną odmienną od innych grup roślin żyjących obecnie, takich jak paprocie, drzewa iglaste i rośliny kwitnące. Sugeruje się, że spirale Fibonacciego pojawiały się osobno kilka razy podczas ewolucji roślin.
Praca dodaje również kolejny element do układanki głównego pytania ewolucyjnego – dlaczego spirale Fibonacciego są tak powszechne w dzisiejszych roślinach?
To pytanie wciąż budzi kontrowersje wśród naukowców. Zaproponowano różne hipotezy, m.in Zmaksymalizuj ilość światła że każdy otrzymany papier lub Efektywnie pakuj nasiona. Ale nasze odkrycia podkreślają, w jaki sposób spostrzeżenia ze skamieniałości i roślin, takich jak glony, mogą dostarczyć istotnych wskazówek w znalezieniu odpowiedzi.
Sandy’ego Hetheringtonabiolog ewolucyjny roślin, Uniwersytet w Edynburgu I Holly Anna TurnerDoktorant, Paleontologia, Kolegium uniwersyteckie w Cork
Ten artykuł został ponownie opublikowany z Rozmowa Na licencji Creative Commons. Przeczytać Oryginalny artykuł.

„Całkowity miłośnik kawy. Miłośnik podróży. Muzyczny ninja. Bekonowy kujon. Beeraholik.”







More Stories
Prognoza cukrzycy w Australii w 2024 r. | Wiadomości o Mirażu
„Gorąca sauna żabia” pomaga australijskim gatunkom w walce ze śmiercionośnym grzybem
Model sztucznej inteligencji poprawia reakcję pacjentów na leczenie raka