Koło można zamienić w kwadrat za pomocą tego wzoru kirigami | Wiadomości z MIT

Kirigami przenosi wyskakujące książki na zupełnie nowy poziom. Japońskie rzemiosło papiernicze polega na wycinaniu wzorów w papierze, aby przekształcić dwuwymiarowy arkusz papieru w skomplikowaną trójwymiarową strukturę po częściowym złożeniu. W rękach artysty kirigami może tworzyć niezwykle szczegółowe i delikatne repliki struktur natury, architektury i nie tylko.

Naukowcy i inżynierowie również czerpali inspirację z kirigami, stosując zasady od cięcia papieru do projektowania chwytaków robotów, rozciągliwej elektroniki, paneli zbierających wodę oraz innych materiałów i urządzeń zmieniających kształt. W większości te wynalazki są produktami projektowanymi od podstaw. Nie było planu dla inżynierów, aby określić wzór nacięć, które przekształciłyby materiał z jednego pożądanego kształtu w inny — czyli aż do teraz.

A Nowe badanie w Natura nauk obliczeniowych Przedstawia ogólną strategię algorytmiczną, która może rozwiązać dowolną transformację 2D inspirowaną kirigami. Metodę tę można wykorzystać do określenia kąta i długości nacięć, które mają być wykonane, tak aby arkusz mógł przekształcić się z jednego pożądanego kształtu w inny, gdy zostanie otwarty i ściśnięty razem, jak skomplikowana rozszerzalna wstęga.

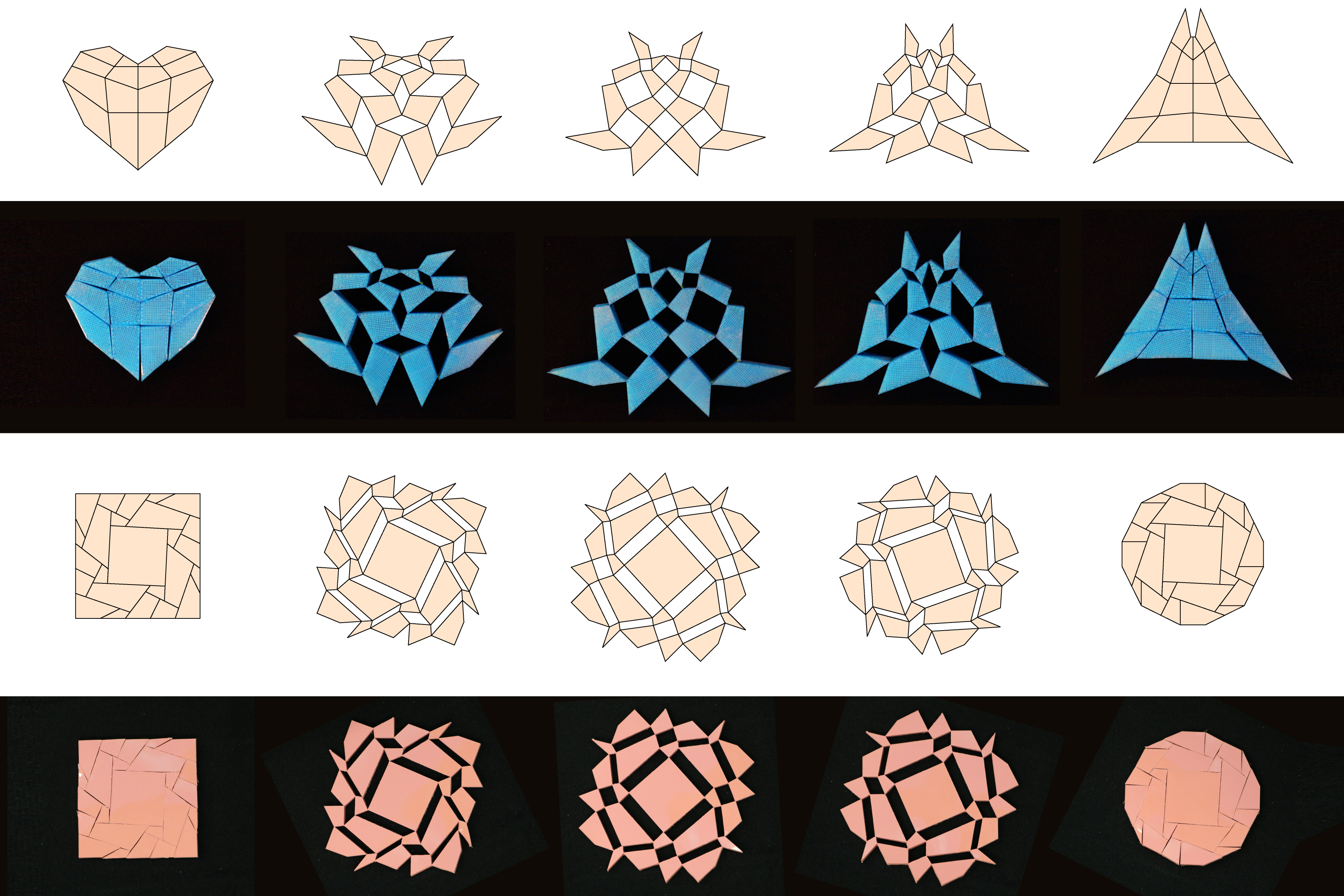
Dzięki nowej metodzie naukowcy zaprojektowali i zbudowali szereg przekształcalnych dwuwymiarowych struktur kirigami, w tym koło, które zamienia się w kwadrat i trójkąt, który zamienia się w serce.

„Ludzie mówili o kwadracie i kole jako o jednym z niemożliwych problemów w matematyce: nie można zamienić jednego w drugi” – mówi Gary Choi, profesor habilitowany i wykładowca matematyki stosowanej na MIT. „Ale dzięki kirigami możemy faktycznie zamienić kwadratowy kształt w kształt koła”.

Dla inżynierów nowa metoda może być wykorzystana do rozwiązywania różnych problemów projektowych, takich jak zaprojektowanie robota, który przekształci się z jednej formy w drugą, aby wykonać określone zadanie lub poruszać się po określonych przestrzeniach. Istnieje również potencjał w zakresie projektowania wydajnych materiałów, na przykład inteligentnych pokryć budynków i domów.

„Jednym z pierwszych zastosowań, o których pomyśleliśmy, były fasady budynków” — mówi Caitlin Baker, adiunkt inżynierii mechanicznej na MIT. „To może pomóc nam tworzyć duże twarze przypominające kirigami, które mogą zmieniać kształt, aby kontrolować światło słoneczne i promieniowanie ultrafioletowe oraz dostosowywać się do otoczenia”.

Baker i Choi są współautorami nowego badania, wraz z Levi Dowdy, badaczem ilościowym w Optiver i L. Mahadevanem, profesorem na Uniwersytecie Harvarda.

przestrzeń pomiędzy

Badanie wyrosło z wcześniejszych prac zespołu nad kirigami i origami — japońską sztuką składania papieru.

„Odkryliśmy, że w kirigami i origami istnieje wiele matematycznych powiązań” – mówi Choi. „Chcieliśmy więc opracować wzór matematyczny, który mógłby pomóc ludziom zaprojektować ogromną różnorodność wzorów”.

W 2019 roku zespół opracował metodę ulepszania kirigami, aby znaleźć wzór nacięć wymaganych do przekształcenia jednego kształtu w inny. Ale Choi mówi, że podejście to było bardzo intensywne obliczeniowo i zajęło dużo czasu, aby uzyskać idealny wzór, aby osiągnąć określoną zmianę.

W 2021 roku naukowcy napotkali podobny problem z origami i odkryli, że dzięki nieco innej soczewce byli w stanie opracować skuteczniejszą strategię. Zamiast wykreślać wzór pojedynczych fałd (podobnie jak w przypadku pojedynczych kawałków kirigami), zespół skupił się na wyhodowaniu wzoru z prostego złożonego ziarna. Pracując płyta po płycie i ustalając relacje między płytami, takie jak ruch jednej płyty, gdyby sąsiednia płyta została złożona, byli w stanie wyprowadzić stosunkowo wydajny algorytm do planowania projektu dowolnej struktury origami.

Zespół zastanawiał się, czy podobne podejście można zastosować do kirigami. W tradycyjnym kirigami, po wykonaniu cięcia w kartce papieru, kartkę można częściowo złożyć, tak aby powstałe puste przestrzenie utworzyły trójwymiarową strukturę. Podobnie jak panele między fałdami origami, czy puste przestrzenie między nacięciami i ich wzajemne relacje mogą dać bardziej wydajną wersję projektu kirigami? To pytanie jest impulsem do nowego badania zespołu.

Linki matematyczne

Badanie koncentruje się na dwuwymiarowych transformacjach kirigami. Naukowcy rozważali ogólny projekt kirigami składający się z mozaiki połączonych ze sobą czworobocznych płytek, z których każda jest cięta pod różnymi kątami iw różnych rozmiarach. Konceptualna mozaika zaczyna się od pojedynczego kształtu i może zostać oddzielona i zsunięta, tworząc zupełnie nowy kształt. Wyzwaniem było opisanie, w jaki sposób jeden kształt może przekształcić się w inny, w oparciu o puste przestrzenie między płytkami i jak przestrzenie zmieniają się, gdy płytki są ciągnięte i zsuwane.

„Jeśli same płytki są solidne i niezmienne, puste przestrzenie między nimi są okazją do ruchu” – mówi Baker.

Zespół najpierw przyjrzał się najprostszej reprezentacji pustej przestrzeni, jako rombowi lub temu, co nazywają „łączem czterotaktowym”. Każdy bok rombu reprezentuje pasek lub krawędź pełnej płytki. Każdy róg rombu reprezentuje ogniwo lub zawias łączący kwadraty. Zmieniając długość i kąt krawędzi rombów, zespół może badać, jak zmienia się pusta przestrzeń między zmianami.

Badając coraz większe grupy czteroprętowych ogniw, zespół określił zależności między kątem i długością prętów, kształtem poszczególnych pustych przestrzeni i kształtem całego zespołu. Przekształcili te zależności w ogólną formułę i odkryli, że może skutecznie określić wzór cięcia — w tym kąt i długość — który byłby wymagany do przekształcenia dwuwymiarowego arkusza papieru z jednego pożądanego kształtu w inny.

„Bez takiego narzędzia mógłbym rozwiązać ten problem brutalnie w Matlabie lub zgadnąć i sprawdzić, ale uzyskanie czegoś, co mogłoby zmienić się z koła w kwadrat, zajęłoby bardzo dużo czasu” — mówi Baker.

W symulacjach zespół odkrył, że formuła może faktycznie znaleźć wzór płytki, który zamieniłby mozaikę w kształcie koła w kwadrat, a także prawie każdy kształt w dowolny inny pożądany kształt.

Idąc dalej, zespół opracował dwie metody produkcji, aby faktycznie zrealizować projekty receptur. Wkrótce zdali sobie sprawę, że głównym wyzwaniem przy tworzeniu ruchomych mozaik było znalezienie odpowiedniego materiału, który będzie działał jako zawiasy fug między płytkami. Połączenia muszą być mocne i łatwe do zginania.

„Pomyślałem, co jest tak mocne na rozciąganie, odporne na rozdarcie, ale może mieć zerowy promień zgięcia, prawie jak precyzyjny zawias?” Baker mówi. I okazuje się, że odpowiedzią jest tkanka.

Zespół zastosował dwie metody — drukowanie 3D i odlewanie ciśnieniowe — aby osadzić małe paski tkaniny w czterostronnych plastikowych płytkach w sposób, który ściśle łączy płytki, jednocześnie pozwalając im opierać się o siebie. Korzystając z tych dwóch metod, zespół stworzył mozaikę kół, które zamieniły się w kwadraty, a także mozaikę prostych trójkątów, które zmieniły się w bardziej złożone kształty serca.

„Możemy przejść do praktycznie dowolnego dwuwymiarowego kształtu” – mówi Choi. „To jest niezawodne, używając naszego wzoru matematycznego. Teraz chcemy rozszerzyć to na 3D kirigami.”